Logistic Regression小结

发表于 2020-04-25 更新于 2020-12-23 分类于计算机科学阅读次数： Valine：

本文字数： 4k 阅读时长 ≈ 4 分钟

Logistic Regression小结

总结一下Logistic Regression。

参考文献：西瓜书，Coursera 《Machine learning》吴恩达

二分类任务

给定数据集\(D=\{(\boldsymbol{x}_i,y_i)\}_{i=1}^m\)，其中\(\boldsymbol{x}_i \in \mathbb{R}^n\)为样本，\(y_i\in \{0,1\}\)分别代表正类和反类的标记。训练一个分类器\(f:\mathbb{R}^n \to \{0,1\}\)。

Logistic Regression是用来解决二分类任务的一种分类器，经过一些修改也可以用作多分类问题。

Logistic Regression的假设函数——对数几率函数

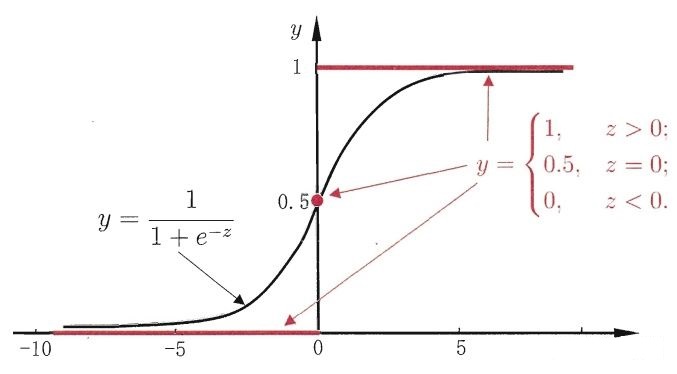
Logistic Regression的想法是用广义线性回归模型来解决二分类问题，首先要找一个假设函数\(f:\mathbb{R}^n \to \{0,1\}\)来做拟合。值域是一个离散的集合\(\{0,1\}\)，最理想的假设函数应当是单位阶跃函数，即

\[ f(x) = \begin{cases} 1, & x>0 \\ 0.5, & x=0 \\ 0, & x<0 \end{cases} \]

很明显，这个函数不光滑甚至不连续，如果用它会出现很多问题。Logistic Regression采用了对数几率函数(logistic function)来替代它：

\[ f(x) = \frac{1}{1+e^{-x}} \]

容易看出对数几率函数的值域是\((0,1)\)，而且它在\(x=0\)处的斜率非常大。（注意：值域中的0和1是取不到的）

给这个对数几率函数加上待训练的参数\(\boldsymbol{w}\)和\(b\)，就得到了我们需要的假设函数：

\[ f(\boldsymbol{x}) = \frac{1}{1 + e^{-( \boldsymbol{w}^T \boldsymbol{x} + b ) }} \]

Logistic Regression的训练方法——极大似然估计

回归问题估计参数一般的方法是最小二乘法，但是注意到这个分类器的值域是取不到\(0\)和\(1\)的，训练集里所有样本的“对数几率”都是无穷，也就是说，最小二乘法失效了。

由此也可以看出，Logistic Regression并不是严格意义上的回归模型，它叫做Regression只是因为历史原因而已。

Logistic Regression里一个关键的处理是把输出\(f(\boldsymbol{x})\)视为样本\(\boldsymbol{x}\)属于正类的概率。用数学来表达就是\(f(\boldsymbol{x}) = P(y=1|\boldsymbol{x})\)。

这样我们就得到了随机变量\(y\in \{0, 1\}\)关于\(\boldsymbol{x}\)的以\(\boldsymbol{w}\)和\(b\)为参数的条件分布：

\[ p(y=1|\boldsymbol{x}) = \frac{e^{\boldsymbol{w}^T \boldsymbol{x}+b}}{1+e^{\boldsymbol{w}^T \boldsymbol{x}+b}} \]

\[ p(y=0|\boldsymbol{x}) = \frac{1}{1+e^{\boldsymbol{w}^T \boldsymbol{x}+b}} \]

接下来用极大似然估计来估计参数\(\boldsymbol{w}\)和\(b\)（这里假设了样本独立同分布），其对数似然函数为 \[ l(\boldsymbol{w},b) = ln(p(\boldsymbol{y}|\mathbf{x})) = ln(\prod_{i=1}^m p(y_i|\boldsymbol{x}_i;\boldsymbol{w},b)) = \sum_{i=1}^m ln(p(y_i|\boldsymbol{x}_i;\boldsymbol{w},b)) \]

然后调整一下记号，并简化一下对数似然函数。

令\(\boldsymbol{\beta} = (\boldsymbol{w};b)\)，\(\hat{\boldsymbol{x}} = (\boldsymbol{x};1)\)，则有\(\boldsymbol{w}^T\boldsymbol{x}+b=\boldsymbol{\beta}^T\boldsymbol{x}\)。再记\(p_1(\hat{\boldsymbol{x}};\boldsymbol{\beta}) = p(y=1|\hat{\boldsymbol{x}},\boldsymbol{\beta})\) ，\(p_0(\hat{\boldsymbol{x}};\boldsymbol{\beta}) = p(y=0|\hat{\boldsymbol{x}},\boldsymbol{\beta})\)

注意到\(y\in \{0,1\}\)，则对数似然函数可简化为： \[ l(\boldsymbol{w},b) = \sum_{i=1}^m ln((y_i p_1(\hat{\boldsymbol{x}};\boldsymbol{\beta})) + (1-y_i)p_0(\hat{\boldsymbol{x}};\boldsymbol{\beta})) \]

最大化对数似然函数可等价于最小化其相反数，将\(y\)的条件带入后可得到如下优化问题： \[ (w^*, \boldsymbol{\beta}^*) = \arg \min_{w,\boldsymbol{\beta}} \sum_{i=1}^m(-y_i\boldsymbol{\beta}^T\hat{\boldsymbol{x}_i}+ln(1+e^{\boldsymbol{\beta}^T\boldsymbol{\hat{x}_i}})) \]

可以证明\(l(w, \boldsymbol{\beta})\)是凸函数，可以使用数值优化算法如牛顿法、梯度下降法等求得最优解。

Logistic Regression的损失函数——交叉熵

对数似然函数\(l(\boldsymbol{w},b)\)还有另外一种化简的方法： \[ l(\boldsymbol{w},b) = \sum_{i=1}^m ln(p_1(\hat{\boldsymbol{x}};\boldsymbol{\beta})^{y_i}p_0(\hat{\boldsymbol{x}};\boldsymbol{\beta})^{(1-y_i)}) = \sum_{i=1}^m y_iln(p_1(\hat{\boldsymbol{x}};\boldsymbol{\beta}))+(1-y_i)ln(p_0(\hat{\boldsymbol{x}};\boldsymbol{\beta})) \] 用这种化简方法同样可以推导出上面的最小化问题。可以看到，Logistic Regression采用的损失函数是交叉熵（cross entropy） \[ Cost(f(\boldsymbol{x}), y) = -yln(f(\boldsymbol{x})) - (1-y)ln(1-f(\boldsymbol{x})) \] 代价函数\(J\)为对数似然函数的相反数\(-l(\boldsymbol{w},b)\)： \[ J = \sum_{i=1}^m Cost(f(\boldsymbol{x_i}), y_i) = \sum_{i=1}^m (-y_iln(f(\boldsymbol{x_i})) - (1-y_i)ln(1-f(\boldsymbol{x_i}))) = -l(\boldsymbol{w},b) \] 研究交叉熵损失\(Cost(f(\boldsymbol{x}), y)\)关于\(f(\boldsymbol{x})\)在一维情形\(x\in \mathbb{R}\)的图像容易发现，它的性质是：

当\(y=1\)时，如果\(f(x)=1\)，则\(Cost=0\)；如果\(f(x)=0\)，则\(Cost=+\infin\)
当\(y=0\)时，如果\(f(x)=0\)，则\(Cost=0\)；如果\(f(x)=1\)，则\(Cost=+\infin\)

所以交叉熵损失有这样的特点：分类错误的代价为无穷大，分类正确的代价为0.

决策边界

因为我们把Logistic Regression分类器的输出视作属于正类的概率，在类别均衡情况下，分类器的输出大于0.5时将其预测为正类，反之将其预测为反类。

观察\(f(\boldsymbol{x}) = \frac{1}{1 + e^{-( \boldsymbol{w}^T \boldsymbol{x} + b ) }}\)的特点：当\(\boldsymbol{w}^T\boldsymbol{x} + b \ge 0\)时，有\(f(\boldsymbol{x}) \ge 0.5\)；当\(\boldsymbol{w}^T\boldsymbol{x} + b < 0\)时，有\(f(\boldsymbol{x}) < 0.5\)。

而\(\boldsymbol{w}^T\boldsymbol{x} + b = 0\)定义了样本空间\(\mathbb{R}^n\)中的一个超平面，这个超平面被称为决策边界（decision boundary）。在样本空间上得到了Logistic Regression的一种解释：

Logistic Regression实际上是在用一个超平面来划分样本空间，从而分出正反类。
如果希望使用非线性的决策边界，可以把\(\boldsymbol{w}^T\boldsymbol{x} + b\)换为高阶的多项式再进行Logistic Regression。