EM算法和高斯混合模型
EM算法和高斯混合模型
《统计学习方法》对EM算法和GMM的介绍都比较详细,但有不少地方绕弯路,而且记号稍显混乱;《西瓜书》对EM算法和GMM的介绍都非常简洁,有许多细节被略去;B站上的白板推导系列里也有EM算法和GMM详细推导。
为了这次数据挖掘小组作业,在这里整理一下EM和GMM。
EM算法
EM算法是解决含有隐变量情况下的极大似然估计算法
极大似然估计
已知独立同分布数据集\(X = \{x_1,...,x_n\}\),即\(X\stackrel{\text{i.i.d}}{\sim}p(x;\Theta)\)。它们的联合概率密度记为\(p(\mathbf{x};\Theta)\),其中\(\mathbf{x}=(x_1,...,x_n)\)。对参数\(\Theta\)的极大似然估计化归为求解如下问题 \[ \hat{\Theta}_{MLE} = \arg\max_{\theta} ln p(\mathbf{x};\Theta) = \arg\max_{\theta} \sum_{i=1}^n ln p(x_i;\Theta) \] 如果含有隐变量\(z \stackrel{\text{i.i.d}}{\sim}q(z;\Theta)\),隐含数据集记为\(Z = \{z_1,...,z_n\}\),它们的联合概率密度记为\(q(\mathbf{z};\Theta)\),其中\(\mathbf{z}=(z_1,...,z_n)\),此时MLE变为求解如下问题 \[ \begin{gather*} \hat{\Theta}_{MLE} = \arg\max_{\Theta} ln p(\mathbf{x};\Theta) = \arg\max_{\Theta} ln\int_{\mathbf{z}} p(\mathbf{x},\mathbf{z};\Theta) d\mathbf{z} \\ = \arg\max_{\Theta} ln \int_\mathbf{z} p(\mathbf{z};\Theta) p(\mathbf{x}|\mathbf{z};\Theta) d\mathbf{z} =\arg\max_{\Theta} \int_\mathbf{z} p(\mathbf{z};\Theta) p(\mathbf{x}|\mathbf{z};\Theta) d\mathbf{z} \\ \end{gather*} \] 因隐含数据集\(Z = \{z_1,...,z_n\}\)无法观测到,联合概率密度\(p(\mathbf{z};\Theta)\)无法计算,无法求解上述问题
对数似然函数的下界
在有隐变量\(Z\)的情况下,为了最大化对数似然函数\(ln p(\mathbf{x};\Theta)\),先对它做一些变形
假设\(q(z)\)是隐变量\(Z\)服从的概率分布,\(q(\mathbf{z})\)是对应的联合概率密度,则有 \[ lnp(\mathbf{x};\Theta) = ln\int_{\mathbf{z}} p(\mathbf{x},\mathbf{z};\Theta) d\mathbf{z} = ln\int_{\mathbf{z}}\frac{p(\mathbf{x},\mathbf{z};\Theta)}{q(\mathbf{z})}q(\mathbf{z}) d\mathbf{z} \] 然后用Jensen不等式进行放缩 \[ lnp(\mathbf{x};\Theta) = ln\int_{\mathbf{z}}\frac{p(\mathbf{x},\mathbf{z};\Theta)}{q(\mathbf{z})}q(\mathbf{z}) d\mathbf{z} \ge \int_{\mathbf{z}} ln\frac{p(\mathbf{x},\mathbf{z};\Theta)}{q(\mathbf{z})} q(\mathbf{z}) d\mathbf{z} \] 这就得到了对数似然函数\(ln p(\mathbf{x};\Theta)\)的下界 \[ ln p(\mathbf{x};\Theta) \ge \int_{\mathbf{z}} ln\frac{p(\mathbf{x},\mathbf{z};\Theta)}{q(\mathbf{z})}q(\mathbf{z}) d\mathbf{z} \]
由Jensen不等式的性质知,等号成立当且仅当 \[ p(\mathbf{x}, \mathbf{z};\Theta) = Cq(\mathbf{z}) \] 两边对\(\mathbf{z}\)积分可得 \[ \int_{\mathbf{z}} p(\mathbf{x},\mathbf{z};\Theta) d\mathbf{z} = C \int_{\mathbf{z}} q(\mathbf{z}) d\mathbf{z} \] 因为\(q(\mathbf{z})\)是概率密度函数,积分是1;\(p(\mathbf{x},\mathbf{z};\Theta)\)对\(\mathbf{z}\)积分是边缘概率密度\(p(\mathbf{x};\Theta)\)。由此可知\(C=p(\mathbf{x};\Theta)\),所以 \[ q(\mathbf{z}) = \frac{p(\mathbf{x},\mathbf{z};\Theta)}{C} = \frac{p(\mathbf{x},\mathbf{z};\Theta)}{p(\mathbf{x};\Theta)} = p(\mathbf{z}|\mathbf{x};\Theta) \] 即\(q(\mathbf{z})\)是观测到数据集\(\mathbf{x}\)后的后验分布。这也启发了EM算法选取\(q(\mathbf{z})\)的原因。
EM算法的导出
我们把真实参数记为\(\Theta\),EM算法第\(t\)步迭代时得到的参数近似值记为\(\Theta^{(t)}\)
EM算法把第\(t\)步迭代时以当前参数估计值\(\Theta^{(t)}\)的\(\mathbf{z}\)的后验分布作为\(q(\mathbf{z})\),即\(q(\mathbf{z}) = p(\mathbf{z}|\mathbf{x};\Theta^{(t)})\),这样就得到了第\(t\)步迭代时对数似然的下界,记为\(B(\Theta,\Theta^{(t)})\) \[ ln p(\mathbf{x};\Theta) \ge \int_{\mathbf{z}} ln\frac{p(\mathbf{x},\mathbf{z};\Theta)}{p(\mathbf{z}|\mathbf{x};\Theta^{(t)})}p(\mathbf{z}|\mathbf{x};\Theta^{(t)}) d\mathbf{z} = B(\Theta,\Theta^{(t)}) \] 为了最大化对数似然函数,EM算法对它的下界\(B(\Theta,\Theta^{(t)})\)进行最大化,求解得到的参数作为下一步迭代的参数\(\Theta^{(t+1)}\) \[ \Theta^{(t+1)} = \arg\max_{\Theta} B(\Theta,\Theta^{(t)}) = \arg\max_{\Theta} \int_\mathbf{z} ln \frac{p(\mathbf{x},\mathbf{z};\Theta)}{p(\mathbf{z}|\mathbf{x};\Theta^{(t)})} p(\mathbf{z}|\mathbf{x};\Theta^{(t)}) d\mathbf{z} \] 展开对数项后,注意到\(p(\mathbf{z}|\mathbf{x};\Theta^{(t)})\)关于\(\Theta\)是常数,上面的迭代公式可化为 \[ \Theta^{(t+1)} = \arg\max_{\Theta} B(\Theta,\Theta^{(t)}) = \arg\max_{\Theta} \int_\mathbf{z} ln p(\mathbf{x},\mathbf{z};\Theta) p(\mathbf{z}|\mathbf{x};\Theta^{(t)}) d\mathbf{z} = \arg\max_{\Theta}Q(\Theta,\Theta^{(t)}) \] 这就是EM算法最终的迭代公式,通常把最后的积分项记为\(Q(\Theta,\Theta^{(t)})\),称为Q函数
- 经过这一系列的迭代,每一步选取的\(\Theta\)都使下界\(B(\Theta,\Theta^{(t)})\)得到增大,迫使对数似然函数也被增大。再由单调有界原理可以证明EM算法将会收敛到一个局部极大值点。
下图是《统计学习方法》的插图,解释了EM算法的迭代过程
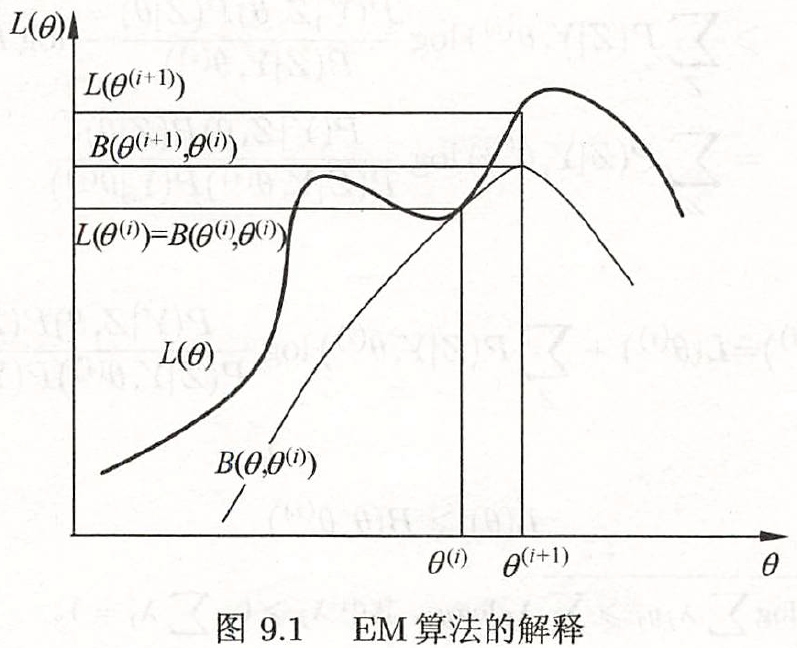
如果将积分项写成数学期望,则迭代公式还可写作 \[ \Theta^{(t+1)} = \arg\max_{\Theta} \mathbb{E}_{\mathbf{z|\mathbf{x};\Theta^{t}}} [lnp(\mathbf{x},\mathbf{z};\Theta)] \] 可以看到这个迭代公式分两步,第一步求期望,第二步求最大化,这也是EM算法(Expectation-Maximum)名字的由来
总结一下,EM算法分为E步(求期望步)和M步(最大化步):
- 使用当前步估计的参数\(\Theta^{(t)}\),求对数似然函数关于\(\mathbf{z}\)的期望\(\mathbb{E}_{\mathbf{z|\mathbf{x};\Theta^{t}}} [lnp(\mathbf{x},\mathbf{z};\Theta)]\)
- 最大化对数似然函数的期望,求得参数\(\Theta^{(t+1)}\)作为下一步迭代的参数
EM算法的收敛性
正如前文所言,EM算法的迭代使对数似然的下界\(B(\Theta,\Theta^{(t)})\)不断增大,从而迫使对数似然函数增大。因此只需要证明\(lnp(\mathbf{x};\Theta^{(t)})\)关于迭代次数\(t\)单调递增,再用单调有界原理即可证明算法收敛。
下面证明\(lnp(\mathbf{x};\Theta^{(t)})\)单调递增: \[ lnp(\mathbf{x};\Theta) = lnp(\mathbf{x},\mathbf{z};\Theta) - lnp(\mathbf{z}|\mathbf{x};\Theta) \] 两边对概率分布\(p(\mathbf{z}|\mathbf{x};\Theta^{(t)})\)取期望,注意到\(lnp(\mathbf{x};\Theta)\)和\(\mathbf{z}\)无关 \[ lnp(\mathbf{x};\Theta) = \int_\mathbf{z} lnp(\mathbf{x},\mathbf{z};\Theta) p(\mathbf{z}|\mathbf{x};\Theta^{(t)}) d\mathbf{z} - \int_\mathbf{z} lnp(\mathbf{z}|\mathbf{x};\Theta) p(\mathbf{z}|\mathbf{x};\Theta^{(t)}) d\mathbf{z} \] 等式右边第一项就是\(Q(\Theta, \Theta^{(t)})\),第二项我们记为\(H(\Theta, \Theta^{(t)})\)
作差比大小: \[ lnp(\mathbf{x};\Theta^{(t+1)}) - lnp(\mathbf{x};\Theta^{(t)}) = [Q(\Theta^{(t+1)},\Theta^{(t)}) - Q(\Theta^{(t)},\Theta^{(t)})] + [H(\Theta^{(t)},\Theta^{(t)}) - H(\Theta^{(t+1)}, \Theta^{(t)})] \] 因为\(\Theta^{(t+1)} = \arg\max_\Theta Q(\Theta, \Theta^{(t)})\),自然有\(Q(\Theta^{(t+1)},\Theta^{(t)}) \ge Q(\Theta^{(t)},\Theta^{(t)})\),所以等号右边第一项非负
再来看右边第二项 \[ \begin{gather*} H(\Theta^{(t)},\Theta^{(t)}) - H(\Theta^{(t+1)}, \Theta^{(t)}) = -\int_{\mathbf{z}} ln\frac{p(\mathbf{z}|\mathbf{x};\Theta^{(t+1)})}{p(\mathbf{z}|\mathbf{x};\Theta^{(t)})} p(\mathbf{z}|\mathbf{x};\Theta^{(t)}) d\mathbf{z} \\ \ge -ln\int_{\mathbf{z}} \frac{p(\mathbf{z}|\mathbf{x};\Theta^{(t+1)})}{p(\mathbf{z}|\mathbf{x};\Theta^{(t)})} p(\mathbf{z}|\mathbf{x};\Theta^{(t)}) d\mathbf{z} = -ln1 = 0 \end{gather*} \] 这说明第二项也是非负的,所以我们证明了 \[ lnp(\mathbf{x};\Theta^{(t+1)}) - lnp(\mathbf{x};\Theta^{(t)}) \ge 0 \] 再由单调有界原理可知,\(lnp(\mathbf{x};\Theta^{(t)})\)最终会收敛到某一值
更进一步可以证明EM算法得到的参数估计序列\(\Theta^{(t)}\)会收敛到某个稳定点\(\hat{\Theta}\),这里不再深入。
- EM算法容易受初值影响,只能收敛到局部极大值点而不能收敛到全局最大值点
高斯混合模型(GMM)
用高斯分布对数据集建模
混合高斯模型(Gaussian Mixture Model)使用\(K\)个高斯分布的加权和对数据集进行建模,认为观测数据分两步生成:
- 由离散型随机变量\(z\)选择数据属于哪个成分,\(z\)的概率分布是\(P(z=k)=\alpha_k\);
- 假设选出的是第\(k\)个成分,在第\(k\)个高斯分布中采样得到一个观测数据,重复\(n\)次这样的操作得到整个数据集\(\mathbf{x} = \{x_1,..,x_n\}\)
如果数据的生成过程看作上述两步的话,整个数据集服从的分布就是高斯分布的加权和 \[ p_{M}(x;\Theta) = \sum_{z} p(x,z) = \sum_{k=1}^K p(x|z)P(z=k)= \sum_{k=1}^K \alpha_k\phi(x;\mu_k,\sigma_k^2) \] 其中\(\phi\)是高斯分布的概率密度函数,\(\Theta\)是所有参数,即\(\Theta = (\mathbf{\alpha},\mathbf{\mu},\mathbf{\sigma^2})\)。\(\mu_k,\sigma_k^2\)是第\(k\)个高斯分布成分的均值和方差,即 \[ \phi(x;\mu_k,\sigma_k^2) = \frac{1}{\sqrt{2\pi}\sigma_k} e^{-\frac{(x-\mu_k)^2}{2\sigma_k^2}} \]
用EM算法进行参数估计
概率分布\(p_{M}(x;\Theta)\)中需要估计的参数是
\(\mathbf{\alpha}=(\alpha_1,...,\alpha_K),\mathbf{\mu}=(\mu_1,...,\mu_K),\mathbf{\sigma^2}=(\sigma_1^2,...,\sigma_K^2)\)
由于随机变量\(z\)无法被观测到,只能通过EM算法进行求解:
E-Step
记概率分布的真实参数\(\Theta = (\mathbf{\alpha},\mathbf{\mu},\mathbf{\sigma^2})\),记算法第\(t\)步迭代时估计的参数近似值为\(\Theta^{(t)} = (\mathbf{\mu}^{(t)},\mathbf{\sigma^{(t)}},\mathbf{\alpha^{(t)}})\)
先写出完整数据\((X,Z)\)的似然函数 \[ p(\mathbf{x},\mathbf{z};\Theta) = \prod_{k=1}^K \prod_{i=1}^n [\alpha_k \phi(x_i;\mu_k,\sigma_k^2)]^{z_{ik}} = \prod_{k=1}^K \prod_{i=1}^n [\alpha_k \frac{1}{\sqrt{2\pi}\sigma_k} e^{-\frac{(x_i-\mu_k)^2}{2\sigma_k^2}}]^{z_{ik}} \] 这里\(z_{ik}\)是0-1随机变量,即示性函数\(z_{ik}=\mathbb{I}(z_i=k)\),表示第\(i\)个数据\(x_i\)是否来自第\(k\)个高斯成分 \[ z_{ik}= \begin{cases} 1, & z_i =k \\ 0, & z_i \ne k \end{cases} \] 再写出完整数据\((X,Z)\)的对数似然函数 \[ lnp(\mathbf{x},\mathbf{z};\Theta) = \sum_{k=1}^K \sum_{i=1}^n z_{ik}[ln\alpha_k - ln\sqrt{2\pi}-ln\sigma_k -\frac{(x_i-\mu_k)^2}{2\sigma_k^2} ] \] 再写出\(Q\)函数 \[ \begin{gather*} Q(\Theta,\Theta^{(t)})= \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}} [lnp(\mathbf{x},\mathbf{z};\Theta)] \\ = \sum_{k=1}^K \sum_{i=1}^n \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}][ln\alpha_k - ln\sqrt{2\pi}-ln\sigma_k -\frac{(x_i-\mu_k)^2}{2\sigma_k^2} ] \end{gather*} \] 为了方便以下叙述,这里先计算\(\mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}]\) \[ \begin{gather*} \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}] = P(z_i=k|{x_i};\Theta^{(t)}) = \frac{P(z_i=k,x_i;\Theta^{(t)})}{p(x_i;\Theta^{(t)})} = \frac{P(z_i=k,x_i;\Theta^{(t)})}{\sum_{k=1}^K P(x_i,z_i=k;\Theta^{(t)})} \\ = \frac{p(x_i|z_i=k;\Theta^{(t)})P(z_i=k;\Theta^{(t)})}{\sum_{k=1}^K p(x_i|z_i=k;\Theta^{(t)})P(z_i=k;\Theta^{(t)})} = \frac{\alpha_k^{(t)}\phi(x_i;\Theta_k^{(t)})}{\sum_{k=1}^K \alpha_k^{(t)}\phi(x_i;\Theta_k^{(t)}) } \end{gather*} \]
M-Step
为求解\(\Theta^{(t+1)} = \arg\max_{\Theta}Q(\Theta,\Theta^{(t)})\),只需分别令\(Q\)函数对\(\mu_k,\sigma_k^2,\alpha_k\)偏导数为0
求导时需注意到\(\mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}]\)的表达式与\(\mu_k,\sigma_k^2,\alpha_k\)都无关
先令\(Q\)对\(\mu_k\)的偏导数为0 \[ \frac{\partial Q(\Theta,\Theta^{(t)})}{\partial \mu_k} = \sum_{i=1}^n\mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}] \frac{x_i - \mu_k}{\sigma_k^2} = 0 \] 化简得到 \[ \mu_k^{(t+1)} = \frac{\sum_{i=1}^n \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}]x_i}{\sum_{i=1}^n \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}]} \]
再令\(Q\)对\(\sigma_k^2\)的偏导数为0 \[ \frac{\partial Q(\Theta,\Theta^{(t)})}{\partial \sigma_k^2} = \sum_{i=1}^n \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}] \frac{(x_i - \mu_k)^2 - \sigma_k^2}{2\sigma_k^4} = 0 \] 化简得到 \[ {\sigma_k^{2}}^{(t+1)} = \frac{\sum_{i=1}^n \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}] (x_i-\mu_k)^2}{\sum_{i=1}^n \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}]} \] 最后求解\(\alpha_k^{(t+1)}\),注意需要满足约束条件\(\sum_{k=1}^K \alpha_k = 1\),因此用拉格朗日乘子法求解 \[ L = Q(\Theta, \Theta^{(t)}) + \lambda (\sum_{k=1}^K \alpha_k -1) \]
\[ \frac{\partial L}{\partial \alpha_k} = \lambda + \frac{1}{\alpha_k}\sum_{i=1}^n \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}] = 0 \]
化简得 \[ \alpha_k^{(t+1)} = \frac{-\sum_{i=1}^n \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}]}{\lambda} \] 加上约束条件\(\sum_{k=1}^K \alpha_k = 1\)可得 \[ -\sum_{k=1}^K \sum_{i=1}^n \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}] = \lambda \] 注意到\(\sum_{k=1}^K \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}] = 1\),所以\(\lambda = -n\) \[ \alpha_k^{(t+1)} = \frac{\sum_{i=1}^n \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}]}{n} \] 这样就得到了GMM最终的迭代公式 \[ \begin{gather*} \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}] = \frac{\alpha_k^{(t)}\phi(x_i;\Theta_k^{(t)})}{\sum_{k=1}^K \alpha_k^{(t)}\phi(x_i;\Theta_k^{(t)}) } \\ \mu_k^{(t+1)} = \frac{\sum_{i=1}^n \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}]x_i}{\sum_{i=1}^n \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}]} \\ {\sigma_k^{2}}^{(t+1)} = \frac{\sum_{i=1}^n \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}] (x_i-\mu_k)^2}{\sum_{i=1}^n \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}]} \\ \alpha_k^{(t+1)} = \frac{\sum_{i=1}^n \mathbb{E}_{\mathbf{z}|\mathbf{x};\Theta^{(t)}}[z_{ik}]}{n} \end{gather*} \] 模型训练结束后可用来进行聚类,因为\(z_{ik}\)是指示数据\(x_i\)是否来自于第\(k\)个高斯成分的随机变量,可以使用\(z_{ik}\)的数学期望作为数据\(x_i\)的类标记 \[ \lambda_i = \arg\max_k \mathbb{E}_{\mathbf{z}|\mathbf{x};\hat{\Theta}}[z_{ik}] \] 下面是西瓜书给出的高斯混合聚类算法伪代码,和本文记号有一点区别

参考文献
周志华. 机器学习. 北京: 清华大学出版社, 2016. Print.
李航. 统计学习方法(第2版). 清华大学出版社, 2019. Print.